Integral Tak Wajar

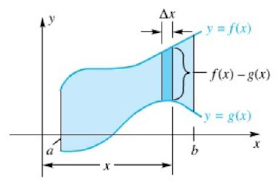
Sebelumnya, kita telah membahas mengenai teorema dasar kalkulus. Coba kita kembali memperhatikan teorema tersebut.

Teorema:

Misal `f(x)` adalah fungsi yang kontinu dan terintegralkan pada `I = [a,b]`, dan `F(x)` sebarang antiturunan pada I, maka

`\int_{a}^{b}f(x)dx=[F(x)]_{a}^{b}=F(b)-F(a)`

Nah, sekarang coba teman-teman perhatikan contoh-contoh berikut.

1) `\int_2^4(1-x) dx=[x-\frac{1}{2} x^2]_2^4`

`=(4-\frac{1}{2}.16)-(2-\frac{1}{2}.4)`

`=-4-0`

`=-4`

2) `\int_1^2 \frac{dx}{1+x}=[\ln |1+x|]_1^2`

`=\ln (1+2)-\ln (1+1)`

`=\ln 3-\ln 2`

3) `\int_1^2 \frac{d x}{\sqrt{1-x}}` tidak dapat diselesaikan dengan teorema di atas karena integran `f(x)=\frac{1}{\sqrt{1-x}}` tidak terdefinisi pada `x=1`.

4) `\int_{-1}^{1}\frac{dx}{x}` juga tidak dapat diselesaikan dengan teorema di atas karena integran `f(x)=\frac{1}{x}` tidak terdefinisi di `x=0`

Dengan demikian tidak semua integral fungsi dapat diselesaikan dengan teorema dasar kalkulus. Persoalan-persoalan integral seperti pada contoh 3 dan 4 dikategorikan sebagai integral tidak wajar.

Bentuk `\int_{a}^{b}f(x)dx` disebut Integral Tidak Wajar jika:

a. Integran `f(x)` mempunyai sekurang-kurangnya satu titik yang tidak kontinu (diskontinu) di `[a,b]`, sehingga `f(x)` tidak terdefinisi di titik tersebut. Pada kasus ini teorema dasar kalkulus yaitu `\int_{a}^{b}f(x)dx=F(b)-F(a)` tidak berlaku lagi.

Contoh: 

1. `\int_{0}^{4}\frac{dx}{4-x}`, `f(x)` tidak kontinu di batas atas `x = 4` atau `f(x)` kontinu di `[0,4)`

2. `\int_{1}^{2}\frac{dx}{\sqrt{x-1}}`, `f(x)` tidak kontinu di batas bawah `x = 1` atau `f(x)` kontinu di `(1,2]`

3. `\int_{0}^{4}\frac{dx}{(2-x)^{\frac{2}{3}}}`, `f(x)` tidak kontinu di `x=2\in [0,4]` atau `f(x)` kontinu di `[0,2)\cup (2,4]`

b. Batas integrasinya paling sedikit memuat satu tanda tak hingga.

Contoh:

1. `\int_{0}^{\infty}\frac{dx}{x^{2}+4}`, integran `f(x)` memuat batas atas di `x=\infty`

2. `\int_{-\infty }^{0}e^{2x}dx`, integran `f(x)` memuat batas bawah di `x=-\infty`

3. `\int_{-\infty}^{\infty}\frac{dx}{1+4x^{2}}`, integran `f(x)` memuat batas atas di `x=\infty` dan batas bawah di `x=-\infty`

Pada contoh a (1, 2, 3) adalah integral tak wajar dengan integran `f(x)` tidak kontinu dalam batas-batas pengintegralan, sedangkan pada contoh b (1, 2, 3) adalah integral tak wajar karena integran `f(x)` mempunyai batas di tak hingga (`\infty`). Integral tak wajar selesaiannya dibedakan menjadi integral tak wajar dengan integran tidak kontinu dan integral tak wajar dengan batas integrasi di tak hingga.

Integral tak wajar dengan integran diskontinu

A. `f(x)` kontinu di `[a,b)` dan tidak kontinu di `x = b`

Karena `f(x)` tidak kontinu di `x = b`, maka sesuai dengan syarat dan definsi integral tertentu integrannya harus ditunjukkan kontinu di `x=b-\varepsilon` `(\varepsilon \rightarrow 0^{+})`,sehingga

`\int_a^b f(x) dx=\lim _{\varepsilon \rightarrow 0^{+}} \int_a^{b-\varepsilon} f(x) dx`

Atau kita juga dapat mencari nilai suatu integral tak wajar dengan cara berikut.

Karena batas atas `x=b-\varepsilon` `(x \rightarrow b^{-})` maka

`\int_a^b f(x) d x=\lim _{t \rightarrow b^{-}} \int_a^t f(x) d x`

Perhatikan contoh berikut agar teman-teman dapat memahami rumus di atas dengan baik.

1. `\int_0^4 \frac{d x}{\sqrt{4-x}}`, `f(x)` tidak kontinu di batas atas `x=4` sehingga 

`\int_0^4 \frac{d x}{\sqrt{4-x}}=\lim _{\varepsilon \rightarrow 0^{+}} \int_0^{4-\varepsilon} \frac{d x}{\sqrt{4-x}}`

`=[\lim _{\varepsilon \rightarrow 0^{+}}-2 \sqrt{4-x}\right]_0^{4-\varepsilon}`

`=-2 \lim _{\varepsilon \rightarrow 0^{+}}[\sqrt{4-(4-\varepsilon)}-\sqrt{4-0}]`

`=-2(\lim _{\varepsilon \rightarrow 0^{+}} \sqrt{\varepsilon}-\sqrt{4})`

`=-2 (0-2)`

`=4`

Cara lain:

`\int_0^4 \frac{d x}{\sqrt{4-x}}=\lim _{t \rightarrow 4^{-}} \int_0^t \frac{d x}{\sqrt{4-x}}`

`=\lim _{t \rightarrow 4^{-}}[-2 \sqrt{4-x}]_{0}^{t}`

`=\lim _{t \rightarrow 4^{-}} [-2 \sqrt{4-t}+2 \sqrt{4-0}]`

`=-2(0)+2(2)`

`=4`

2. `\int_{-2}^2 \frac{d x}{\sqrt{4-x^2}},f(x)=\frac{1}{\sqrt{4-x^2}}`

Fungsi di atas tidak kontinu di `x=2` dan `x=-2`, sehingga:

`\int_{-2}^2 \frac{d x}{\sqrt{4-x^2}}=2 \int_0^2 \frac{d x}{\sqrt{4-x^2}}`

`=2[\lim_{\varepsilon \rightarrow 0^{+}} \arcsin \frac{x}{2}]_0^{2-\varepsilon}`

`=2\lim_{\varepsilon \rightarrow 0^{+}} [\arcsin \frac{2-\varepsilon }{2}-\arcsin 0]`

`=2(\arcsin 1-\arcsin 0)`

`=2(\frac{\pi}{2}-0)`

`=\pi`

3. `\int_0^4 \frac{d x}{(4-x)^{\frac{3}{2}}}=\lim_{\varepsilon \rightarrow 0^{+}} [\frac{2}{\sqrt{4-x}}]_0^{4-\varepsilon}`, `f(x)` tidak kontinu di batas atas `x=4` sehingga diperoleh

`\int_{0}^{4} \frac{d x}{(4-x)^{\frac{3}{2}}}=\lim _{\varepsilon \rightarrow 0^{+}}\left[\frac{2}{\sqrt{4-(4-\varepsilon)}}-\frac{2}{\sqrt{4-0}}\right]`

= tidak berarti, karena mempunyai bentuk `\frac{2}{0}`

B. `f(x)` kontinu di `(a,b]` dan tidak kontinu di `x = a`

Karena `f(x)` tidak kontinu di `x = a`, maka sesuai dengan syarat dan definsi integral tertentu integrannya harus ditunjukkan kontinu di `x=a+\varepsilon` `(\varepsilon \rightarrow 0^{+})`, sehingga

`\int_a^b f(x) d x=\lim_{\varepsilon \rightarrow 0^{+}} \int_{a+\varepsilon}^b f(x) d x`

Atau dengan cara lain, karena batas bawah `x=a+\varepsilon` `(x\rightarrow a^{+})` maka dapat dinyatakan dalam bentuk lain:

`\int_a^b f(x) d x=\lim _{t \rightarrow a^{+}} \int_t^b f(x) d x`

Perhatikan contoh-contoh berikut untuk lebih memahaminya.

1. `\int_3^4 \frac{3 d x}{\sqrt{x-3}}=\lim _{t \rightarrow 3^{+}} \int_t^4 \frac{3 d x}{\sqrt{x-3}}`

`=\lim _{t \rightarrow 3^{+}}[6 \sqrt{x-3}]_t^4`

`=\lim _{t \rightarrow 3^{+}}[6 \sqrt{4-3}-6 \sqrt{t-3}] `

`=6(1)-6(0)`

`=6`

2. `\int_0^1 \frac{d x}{\sqrt{x}}=\lim_{\varepsilon \rightarrow 0^{+}} \int_{0+\varepsilon}^1 \frac{d x}{\sqrt{x}}`, `f(x)` tidak kontinu di batas bawah `x = 0` sehingga diperoleh:

`\int_0^1 \frac{d x}{\sqrt{x}}=\lim_{\varepsilon \rightarrow 0^{+}}[2 \sqrt{x}]_{0+\varepsilon}^1`

`=\lim _{\varepsilon \rightarrow 0^{+}}[2 \sqrt{1}-2 \sqrt{0+\varepsilon}]`

`=2-0`

`=2`

3. `\int_0^1 \ln x d x=\lim_{\varepsilon \rightarrow 0^{+}}[x \ln x-x]_{0+\varepsilon}^1`, `f(x)` tidak kontinu di batas bawah `x=0`

`=\lim _{\varepsilon \rightarrow 0^{+}}[(1 \ln 1-1)-((0+\varepsilon) \ln (0+\varepsilon)-(0+\varepsilon))]`

`=(1.0-1)-(0-0)`

`=-1`

C. `f(x)` kontinu di `[a,c) \cup (c,b]` dan tidak kontinu di `x = c`

Karena `f(x)` tidak terdefinisi di `x = c`, maka sesuai dengan syarat dan definsi integral tertentu integrannya harus ditunjukkan kontinu di `x=c+\varepsilon` dan `x=c-\varepsilon` `(\varepsilon \rightarrow 0^{+})`, sehingga

`\int_a^b f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x`

`=\lim_{\varepsilon \rightarrow 0^{+}} \int_a^{c-\varepsilon} f(x) dx+\lim_{\varepsilon \rightarrow 0^{+}} \int_{c+\varepsilon}^b f(x) dx`

Dapat juga dinyatakan dengan

`\int_a^b f(x) d x=\lim _{t \rightarrow b^{-}} \int_a^t f(x) d x+\lim _{t \rightarrow a^{+}} \int_t^b f(x) dx`

Perhatikan beberapa contoh di bawah ini.

1. `\int_{-1}^8 x^{-\frac{1}{3}} dx`, `f(x)` tidak kontinu `x=0` sehingga diperoleh

`\int_{-1}^0 x^{-\frac{1}{3}} dx+\int_0^8 x^{-\frac{1}{3}} d x =\lim_{\varepsilon \rightarrow 0^{+}} \int_{-1}^{0-\varepsilon} x^{-\frac{1}{3}} d x+\lim_{\varepsilon \rightarrow 0^{+}} \int_{0+\varepsilon}^8 x^{-\frac{1}{3}} dx`

`=\lim_{\varepsilon \rightarrow 0^{+}}[\frac{3}{2} x^{\frac{2}{3}}]_{-1}^{0-\varepsilon}+\lim_{\varepsilon \rightarrow 0^{+}}[\frac{3}{2} x^{\frac{2}{3}}]_{0+\varepsilon}^8`

`=-\frac{3}{2}+6`

`=\frac{9}{2}`

2. `\int_{-1}^1 \frac{d x}{x^4}`, `f(x)` diskontinu di `x=0`, sehingga diperoleh:

`\int_{-1}^1 \frac{d x}{x^4} =\int_{-1}^0 \frac{d x}{x^4}+\int_0^1 \frac{d x}{x^4}`

`=\lim_{\varepsilon \rightarrow 0^{+}} \int_{-1}^{0-\varepsilon} \frac{d x}{x^4}+\lim_{\varepsilon \rightarrow 0^{+}} \int_{0+\varepsilon}^1 \frac{d x}{x^4}`

`=\lim_{\varepsilon \rightarrow 0^{+}}[\frac{-1}{3 x^3}]_{-1}^{0-\varepsilon}+\lim_{\varepsilon \rightarrow 0^{+}}[\frac{-1}{3 x^3}]_{0+\varepsilon}^1`

`=` tidak berarti, karena memuat bentuk `\frac{1}{0}`

Integral tak wajar dengan batas integrasi di tak hingga

Bentuk integral tak wajar dengan batas tak hingga jika sekurang-kurangnya batas-batas integrasinya memuat tak hingga. Selesaiannya berbeda dengan integral tak wajar yang integrannya tidak kontinu di salah satu batas integrasinya.

A. Intergral tak wajar dengan batas atas `x=\infty`.

Selesaiannya cukup dengan mengganti batas atas dengan sebarang variabel dimana variabel tersebut mendekati tak hingga. Dengan demikian integral tak wajar dengan batas atas tak hingga mempunyai selesaian berbentuk

`\int_{a}^{\infty } f(x)dx=\lim_{t\rightarrow \infty }\int_{a}^{t}f(x)dx`

Perhatikan contoh berikut ini.

1. `\int_0^{\infty} \frac{d x}{x^2+4}=\lim _{t \rightarrow \infty} \int_0^t \frac{d x}{x^2+4}`

`=\lim _{t \rightarrow \infty}\left[\frac{1}{2} \arctan \frac{x}{2}\right]_0^t`

`=\lim _{t \rightarrow \infty}[\frac{1}{2} \arctan \frac{t}{2}-\frac{1}{2} \arctan 0]`

`=\frac{1}{2}\arctan(\infty )-\frac{1}{2} \arctan 0`

`=\frac{1}{2} \cdot \frac{\pi}{2}-\frac{1}{2}.0`

`=\frac{\pi}{4}`

2. `\int_1^{\infty} \frac{d x}{x^2}=\lim _{t \rightarrow \infty} \int_1^t \frac{d x}{x^2}`

`=\lim _{t \rightarrow \infty}[-\frac{1}{x}]_1^t`

`=\lim _{t \rightarrow \infty}[-\frac{1}{t}+1]`

`=-\frac{1}{\infty }+1`

`=0+1`

`=1`

B. Integral tak wajar dengan batas bawah di `x=-\infty`

Selesaiannya cukup dengan mengganti batas bawah dengan sebarang variabel dimana variabel tersebut mendekati (negatif) tak hingga. Dengan demikian, integral tak wajar dengan batas bawah tak hingga mempunyai selesaian:

`\int_{-\infty}^a f(x) d x=\lim _{t \rightarrow-\infty} \int_t^a f(x) d x`

Agar lebih memahaminya perhatikan contoh-contoh berikut.

1. `\int_{-\infty}^0 e^{2 x} dx=\lim _{t \rightarrow-\infty}[\frac{1}{2} e^{2 x}]_t^0`

`=\lim _{t \rightarrow-\infty}[\frac{1}{2} .1-\frac{1}{2} e^{2 t}]`

`=\frac{1}{2}-0`

`=\frac{1}{2}`

2. `\int_{-\infty}^0 \frac{d x}{(4-x)^2}=\lim _{t \rightarrow-\infty}[\frac{1}{4-x}]_t^0`

`=\lim _{t \rightarrow-\infty}[\frac{1}{4-0}-\frac{1}{4-t}]`

`=\frac{1}{4}-0`

`=\frac{1}{4}`

C. Integral tak wajar batas atas `x=\infty` dan batas bawah di `x=-\infty` 

Khusus untuk bentuk integral ini diubah terlebih dahulu menjadi penjumlahan dua integral tak wajar dengan `\int_{-\infty}^{\infty} f(x) dx=\int_{-\infty}^a f(x) d x+\int_a^{\infty} f(x) d x`, sehingga bentuk penjumlahan integral tak wajar ini dapat diselesaikan dengan cara A dan B seperti di atas, atau diperoleh bentuk:

`\int_{-\infty}^{\infty} f(x) dx =\int_{-\infty}^a f(x) d x+\int_a^{\infty} f(x) d x`

`=\lim _{t \rightarrow-\infty} \int_t^a f(x) d x+\lim _{t \rightarrow \infty} \int_a^t f(x) d x`

Perhatikan contoh di bawah ini:

1. `\int_{-\infty}^{\infty} \frac{d x}{1+4 x^2}=\int_{-\infty}^0 \frac{d x}{1+4 x^2}+\int_0^{\infty} \frac{d x}{1+4 x^2}`

`=\lim _{t \rightarrow-\infty}[\frac{arctan (2x)}{2}]_t^0+\lim _{t \rightarrow \infty}[\frac{arctan (2x)}{2}]_0^t`

`=\lim _{t \rightarrow-\infty}[0-\frac{arctan (2t)}{2}]+\lim _{t \rightarrow \infty}[\frac{arctan (2t)}{2}-0]`

`=[0-(-\frac{\pi }{4})]+[\frac{\pi }{4}-0]`

`=\frac{\pi }{4}+\frac{\pi }{4}`

`=\frac{\pi }{2}`

Volume Benda Putar-2

 

Pada kesempatan kali ini, kita akan melanjutkan pembahasan kita mengenai volume benda putar. Sebelumnya, kita telah memahami cara menghitung volume benda putar menggunakan metode cakram dan cincin. Selain kedua metode tersebut, teman-teman juga bisa menggunakan metode kulit silinder. Metode kulit silinder sebagai alternatif lain dalam perhitungan volume benda putar yang mungkin lebih mudah diterapkan bila kita bandingkan dengan metode cakram atau metode cincin. Volume benda pejal yang terbentuk oleh perputaran daerah di antara sumbu-x dan grafik fungsi kontinu `y=f(x)\geq 0,L\leq a\leq x\leq b`, mengelilingi sebuah garis vertikal `x=L` adalah

`V=\int_{a}^{b}2\pi` (radius kulit silinder)(tinggi kulit silinder) dx

Andaikan radius kulit silinder = x dan tinggi kulit silinder = f(x) maka:

`V=\int_{a}^{b}2\pi xf(x)dx`

Untuk sumbu putar horizontal (sumbu-y), maka `x` diganti dengan `y` sehingga didapatkan

`V=\int_{a}^{b}2\pi yf(y)dy`

Contoh Soal:

1. Daerah yang dibatasi oleh kurva `y=\sqrt{x}`, sumbu-x, dan garis `x=4` diputar mengelilingi sumbu-y untuk membentuk sebuah benda pejal. Carilah volume benda pejal tersebut. 

Jawab: 

Buatlah sketsa daerah yang dimaksud dan gambarkan sebuah segmen garis yang memotong daerah tersebut yang sejajar dengan sumbu putar (lihat gambar). Berikan label pada tinggi segmen garis (tinggi kulit silinder) dan jarak dari sumbu putar (radius kulit silinder).

Variabel ketebalan kulit silinder adalah `x`, sehingga batas integrasi untuk rumus kulit silinder adalah `a=0` dan `b=4` (lihat gambar). Oleh karena itu, volume benda pejal adalah

`V=\int_{a}^{b}2\pi` (radius kulit silinder)(tinggi kulit silinder) dx

`=\int_{0}^{4}2\pi (x)(\sqrt{x})dx`

`=2\pi\int_{0}^{4}x^{\frac{3}{2}}dx`

`=2\pi[\frac{2x^\frac{5}{2}}{5}]_{0}^{4}`

`=2\pi[\frac{2(4)^\frac{5}{2}}{5}-0]`

`=2\pi[\frac{2(32)}{5}]`

`=\frac{128\pi}{5}`

2. Daerah yang dibatasi oleh kurva `y=\sqrt{x}`, sumbu-x, dan garis `x=4` diputar mengelilingi sumbu-x untuk membentuk sebuah benda pejal. Carilah volume benda pejal dengan metode cangkang silindris.

Jawab:

Pertama, buatlah sketsa daerah dan gambar segmen garis yang memotong daerah yang dimaksud sejajar dengan sumbu putar (lihat gambar). Berikan label pada panjang segmen (tinggi kulit silinder) dan jarak dari sumbu putar (radius kulit silinder).

Pada kasus ini, variabel ketebalan kulit silinder adalah `y`, sehingga batas integrasi untuk rumus metode kulit silinder adalah `a=0` dan `b=2` (sepanjang sumbu-y  pada gambar di atas). Volume benda pejal adalah

`V=\int_{a}^{b}2\pi` (radius kulit silinder)(tinggi kulit silinder) dx

`=\int_{0}^{2}2\pi (y)(4-y^{2})dy`

`=2\pi\int_{0}^{2}(4y-y^{3})dy`

`=2\pi [2y^{2}-\frac{y^{4}}{4}]_{0}^{2}`

`=8\pi`

3. Tentukan volume benda-pejal putar yang terjadi jika daerah `R` dibatasi oleh `x=y^{2}`, `y=2`, `x=0` diputar terhadap garis `y=2`.

Jawab: 

Pertama, kita membuat sketsa daerah dan menggambar segmen garis yang memotong daerah yang dimaksud sejajar dengan sumbu putar (lihat gambar). Berikan label pada panjang segmen (tinggi kulit silinder) dan jarak dari sumbu putar (radius kulit silinder).

 

Pada kasus ini, ketebalan kulit silinder adalah `\Delta y` , sehingga batas integrasi untuk rumus metode kulit silinder adalah `a=0` dan `b=2` (sepanjang sumbu-y  pada gambar di atas). Volume benda pejal adalah

`V=\int_{a}^{b}2\pi` (radius kulit silinder)(tinggi kulit silinder) dx

`V=\int_{0}^{2}2\pi (2-y)(y^{2})dy`

`=2\pi \int_{0}^{2}(2y^{2}-y^{3})dy`

`=2\pi[\frac{2y^{3}}{3}-\frac{y^{4}}{4}]_{0}^{2}`

`=2\pi[\frac{16}{3}-4-0]`

`=2\pi[\frac{4}{3}]`

`=\frac{8\pi }{3}`

Volume Benda Putar-1

Hai hai teman-teman semua...

Pada kesempatan kali ini, kita akan membahas bersama mengenai volume benda putar. Seperti bagaimana sih itu konsep benda putar? Bagaimana metode-metode yang digunakan dalam mencari volume dari benda putar tersebut? Yuk simak penjelasan berikut.

Benda-pejal sederhana yang disebut silinder tegak, empat diantaranya diperlihatkan pada gambar di bawah. Dalam tiap kasus, benda itu dibentuk dengan cara menggerakkan suatu daerah rata (alas) sejauh `h` dengan arah tegak lurus pada daerah tersebut. Dalam tiap kasus, volume benda-pejal didefinisikan sebagai luas alas `A` dikalikan tinggi `h`, yakni

`V=A.h`

Berikut perhatikan sebuah benda-pejal yang penampang-penampangnya tegak lurus dengan suatu garis memiliki luas yang diketahui. Khususnya, misalkan garis tersebut adalah sumbu-x dan misalkan bahwa luas penampang pada `x` adalah `A(x)` dengan `a\leq x\leq b` (lihat gambar di bawah sebelah kiri). Kita partisikan interval `[a,b]` dengan menyisipkan titik-titik `a=x_{0}< x_{1}< x_{2}<...<  x_{i}=b`. Kemudian kita lewatkan bidang-bidang melalui titik-titik ini tegak lurus pada sumbu-x, sehingga mengiris benda menjadi lempengan-lempengan tipis (lihat gambar di bawah sebelah kanan). Volume `\Delta V` suatu lempengan kira-kira sama dengan volume suatu silinder, yakni

`\Delta V_{i}=A(\bar{x_{i}})\Delta x_{i}`

(Ingat bahwa `\bar{x_{i}}` disebut titik sampel, adalah sebarang bilangan dalam interval `[x_{i-1},x_{i}]`)

Volume `V` dari benda-pejal dapat diaproksimasikan dengan jumlah Riemann

`V\approx \sum_{i=1}^{n}A(\bar{x_{i}})\Delta x_{i}`

Ketika norma partisi mendekati nol, diperoleh integral tertentu yang didefinisikan sebagai volume benda-pejal,

`V=\int_{a}^{b}A(x)dx`

Untuk mendapatkan volume benda putar yang terjadi karena suatu daerah diputar terhadap suatu sumbu, dapat dilakukan dengan menggunakan tiga buah metode, yaitu metode cakram, metode cincin, dan metode kulit silinder.

A. Metode Cakram

Benda pejal yang terbentuk karena rotasi (atau revolusi) sebuah daerah bidang mengelilingi sebuah sumbu pada bidangnya disebut benda-putar. Untuk mencari volume sebuah benda pejal dengan metode cakram, kita hanya perlu mengamati bahwa luas penampang `A(x)` adalah luas dari sebuah cakram dengan radius R(x), yaitu jarak batas daerah pada bidang dari sumbu putar. Luasnya dituliskan sebagai berikut:

`A(x)=\pi [R(x)]^{2}`, dengan `R(x)` adalah radius.

Dengan demikian, volume benda-putar mengelilingi sumbu-x berdasarkan metode cakram adalah

`V=\int_{a}^{b}A(x)dx=\int_{a}^{b}\pi [R(x)]^{2} dx`

Untuk mencari volume benda pejal yang dibentuk oleh perputaran suatu daerah di antara sumbu-y dan sebuah kurva `x=R(y), c\leq y\leq d`, mengelilingi sumbu-y, kita gunakan metode yang sama di mana `x` diganti dengan `y`. Pada kasus ini, luas penampang lingkaran adalah

`A(y)=\pi [R(y)]^{2}`, dengan `R(y)` adalah radius.

Sehingga, volume benda-putar mengelilingi sumbu-y berdasarkan metode cakram adalah

`V=\int_{c}^{d}A(y)dy=\int_{c}^{d}\pi [R(y)]^{2} dy`

Agar lebih memahaminya, yuks simak contoh-contoh berikut.

1. Daerah di antara kurva `y=\sqrt{x},0\leq x\leq 4,` dan sumbu-x diputar mengelilingi sumbu-x sehingga membentuk sebuah benda pejal. Tentukan volumenya.

Jawab:

Kita membuat gambar yang menunjukkan daerah yang dimaksud, sebuah radius, dan benda pejal yang terbentuk (lihat gambar).

Berdasarkan gambar, volumenya adalah

`V=\int_{a}^{b}\pi [R(x)]^{2} dx`

`=\int_{0}^{4}\pi [\sqrt{x}]^{2} dx`

`=\pi \int_{0}^{4}x dx`

`=\pi [\frac{x^{2}}{2}]_{0}^{4}`

`=\pi (\frac{4^{2}}{2}-0)`

`=8\pi`

2. Carilah volume benda pejal yang dibentuk oleh perputaran daerah yang dibatasi oleh `y=\sqrt{x}` dan garis-garis `y= 1, x=4` mengelilingi garis `y=1`.

Jawab:

Kita buat gambar yang menunjukkan daerah yang dimaksud, sebuah radius, dan benda pejal yang terbentuk (lihat gambar).

Volume benda pejal adalah

`V=\int_{a}^{b}\pi [R(x)]^{2}dx`

`=\int_{1}^{4}\pi [\sqrt{x}-1]^{2}dx`

`=\pi \int_{1}^{4}[x-2\sqrt{x}+1]dx`

`=\pi [\frac{x^{2}}{2}-2.\frac{2x^{\frac{3}{2}}}{3}+x]_{1}^{4}dx`

`=\pi [(\frac{4^{2}}{2}-2.\frac{2(4^{\frac{3}{2}})}{3}+4)-(\frac{1^{2}}{2}-2.\frac{2(1^{\frac{3}{2}})}{3}+1)]`

`=\pi [\frac{4}{3}-\frac{1}{6}]`

`=\frac{7\pi }{6}`

3. Carilah volume benda pejal yang dibentuk oleh perputaran daerah di antara sumbu-y dan kurva `x=\frac{2}{y},1\leq y\leq 4`, mengelilingi sumbu-y.

Jawab:

Kita buat gambar yang menunjukkan daerah yang dimaksud, sebuah radius, dan benda pejal yang terbentuk (lihat gambar).

Sehingga, volume benda pejal dapat dihitung dengan menggunakan rumus

`V=\int_{c}^{d}\pi [R(y)]^{2}dy`

`=\int_{1}^{4}\pi [\frac{2}{y}]^{2}dy`

`=\pi \int_{1}^{4}\frac{4}{y^{2}}dy`

`=4\pi \int_{1}^{4}\frac{1}{y^{2}}dy`

`=4\pi[-\frac{1}{y}]_{1}^{4}`

`=4\pi (-\frac{1}{4}-(-1))`

`=3\pi`

4. Carilah volume benda pejal yang dihasilkan oleh perputaran daerah di antara parabola `x=y^{2}+1` dan garis `x=3` mengelilingi garis `x=3`.

Jawab:

Kita buat gambar yang menunjukkan daerah yang dimaksud, sebuah radius, dan benda pejal yang terbentuk (lihat gambar). Perhatikan bahwa penampang-penampangnya tegak lurus terhadap garis `x=3` memiliki koordinat `y` dari `y=-\sqrt{2}` sampai `y=\sqrt{2}`.

Dengan demikian, volumenya adalah

`V=\int_{-\sqrt{2}}^{\sqrt{2}} \pi [R(y)]^{2}dy`

`=\int_{-\sqrt{2}}^{\sqrt{2}} \pi [2-y^{2}]^{2}dy`

`=\pi \int_{-\sqrt{2}}^{\sqrt{2}}[4-4y^{2}+y^{4}]dy`

`=\pi [4y-\frac{4y^{3}}{3}+\frac{y^{5}}{5}]_{-\sqrt{2}}^{\sqrt{2}}`

`=\pi[(4(\sqrt{2})-\frac{4(\sqrt{2})^{3}}{3}+\frac{(\sqrt{2})^{5}}{5})-(4(-\sqrt{2})-\frac{4(-\sqrt{2})^{3}}{3}+\frac{(-\sqrt{2})^{5}}{5})]`

`=\pi [\frac{32\sqrt{2}}{15}-(-\frac{32\sqrt{2}}{15})]`

`=\pi [\frac{64\sqrt{2}}{15}]`

`=\frac{64\pi \sqrt{2}}{15}`

B. Metode Cincin

Jika daerah yang kita putar untuk membentuk benda pejal tidak berpotongan dengan sumbu putar, maka benda itu akan memiliki lubang di dalamnya. Jadi, penampang-penampang yang tegak lurus pada sumbu putar merupakan cincin. Luas cincin adalah

`A(x)=\pi [R(x)]^{2}-\pi [r(x)]^{2}=\pi ([R(x)]^{2}-[r(x)]^{2})`

Oleh karena itu, volume benda putar mengelilingi sumbu-x berdasarkan metode cincin adalah

`V=\int_{a}^{b}A(x)dx=\int_{a}^{b}\pi ([R(x)]^{2}-[r(x)]^{2})dx`

Untuk mencari volume benda pejal yang dihasilkan oleh perputaran daerah mengelilingi sumbu-y, kita menggunkan metode yang sama seperti rumus di atas, tetapi melakukan integrasi terhadap `y`. Pada kasus ini ruas garis yang membentuk cincin tegak lurus terhadap sumbu-y (sumbu putar), serta radius luar dan radius dalam merupakan fungsi dari `y`.

`V=\int_{c}^{d}A(y)dy=\int_{c}^{d}\pi ([R(y)]^{2}-[r(y)]^{2})dy`

Contoh Soal:

1. Daerah yang dibatasi oleh kurva `y=x^{2}+1` dan garis `y=-x+3` diputar mengelilingi sumbu-x untuk membentuk benda pejal. Carilah volume benda pejal tersebut.

Jawab:

Pertama, kita menggambar daerah dan membuat sketsa ruas garis yang memotong daerah itu tegak lurus terhadap sumbu putar (ruas garis merah pada gambar).

Kedua, kita mencari radius luar dan radius dalam dari cincin yang terbentuk oleh perputaran ruas garis bersama dengan daerah itu mengelilingi sumbu-x. Kedua radius tersebut adalah jarak antara ujung ruas garis dari sumbu putar (lihat gambar).

Radius luar: `R(x)=-x+3`

Radius dalam: `r(x)=x^{2}+1`

Ketiga, kita mencari batas-batas integrasi dengan mencari koordinat `x` dari titik perpotongan antara kurva dan garis pada gambar di atas.

`x^{2}+1=-x+3`

`\Leftrightarrow x^{2}+x+1-3=0`

`\Leftrightarrow x^{2}+x-2=0`

`\Leftrightarrow (x+2)(x-1)=0`

`\Leftrightarrow x=-2,x=1`

Keempat, kita menghitung volume benda pejal:

`V=\int_{a}^{b}\pi ([R(x)]^{2}-[r(x)]^{2})dx`

`=\int_{-2}^{1}\pi ((-x+3)^{2}-(x^{2}+1)^{2})`

`=\pi \int_{-2}^{1}(8-6x-x^{2}-x^{4})`

`=\pi [8x-3x^{2}-\frac{x^{3}}{3}-\frac{x^{5}}{5}]_{-2}^{1}`

`=\frac{117\pi}{5}`

2. Daerah yang dibatasi oleh parabola `y=x^{2}`  dan garis `y=2x` pada kuadran pertama diputar mengelilingi sumbu-y untuk membentuk benda pejal. Carilah volume benda pejal tersebut.

Jawab:

Pertama, kita sketsakan daerah yang dimaksud dan kita gambar ruas garis yang memotong daerah itu secara tegak lurus terhadap sumbu putar (sumbu-y). Lihat gambar di bawah ini.

Radius cincin yang dibentuk oleh ruas garis adalah:

Radius luar: `R(y)=\sqrt{y}`

Radius dalam: `r(y)=\frac{y}{2}`

Selanjutnya, kita mencari batas-batas integrasi dengan mencari koordinat `y` dari titik perpotongan antara parabola dan garis pada gambar di atas.

`x^{2}=2x`

`\Leftrightarrow x^{2}-2x=0`

`\Leftrightarrow x(x-2)=0`

`\Leftrightarrow x=0,x=2`

Substitusikan nilai `x=0` dan `x=2` ke persamaan parabola `y=x^{2}`, sehingga didapatkan `y=0` dan `y=4`. Garis dan parabola berpotongan pada `y=0` dan `y=4` sehingga batas-batas integrasi adalah `c=0` dan `d=4`. Kita integrasikan untuk mencari volume:

`V=\int_{c}^{d}\pi ([R(y)]^{2}-[r(y)]^{2})dy`

`=\int_{0}^{4}\pi ([\sqrt{y}]^{2}-[\frac{y}{2}]^{2})dy`

`=\pi \int_{0}^{4} (y-\frac{y^{2}}{4})dy`

`=\pi [\frac{y^{2}}{2}-\frac{y^{3}}{12}]_{0}^{4}`

`=\frac{8\pi}{3}`

Luas Daerah Bidang Datar

Pada topik-topik sebelumnya, kita telah membahas mengenai integral tertentu dengan berbagai macam sifatnya. Integral tertentu dapat digunakan untuk menentukan selesaian masalah-masalah praktis dalam kehidupan nyata. Beberapa diantara penggunaan integral adalah menentukan luas suatu luasan, menghitung volume benda pejal, menentukan panjang busur suatu kurva yang telah ditentukan persamaannya, dan menentukan luas permukaan benda putar. Nah, pembahasan kita kali ini secara khusus membahas tentang luas daerah bidang datar.

Luasan didefinisikan sebagai suatu daerah dalam bidang `XOY` dengan persamaan `y=f(x)` atau `x=f(y)`, atau `y=f(x), x=f(y)` yang berbatasan dengan sumbu-sumbu koordinat atau garis yang sejajar sumbu koordinat. Luasan dalam bidang dapat dikelompokkan menjadi luasan positif dan luasan negatif. Luasan positif adalah luasan dengan persamaan `y=f(x)` dan sumbu-sumbu koordinat yang terletak di atas sumbu-x atau luasan dengan persamaan `x=f(y)` dan sumbu-sumbu koordinat yang terletak disebelah kanan sumbu-y. Teman-teman dapat melihat gambar luasan positif yang dimaksud dalam gambar di bawah ini.

Luasan negatif adalah luasan dengan persamaan `y=f(x)` dan sumbu-sumbu koordinat yang terletak di bawah sumbu-x atau luasan dengan persamaan `x=f(y)` dan sumbu-sumbu koordinat yang terletak disebelah kiri sumbu-y. Berikut ini gambar luasan negatif tersebut.

Luasan positif dan negatif sebagaimana telah dijelaskan di atas, pembatasan juga dapat terjadi bukan hanya satu kurva tetapi dapat juga berupa dua kurva sekaligus, misalnya `y_{1}=f(x)` dan `y_{2}=g(x)`. Pembahasan ini diawali dengan menentukan luas luasan menggunakan integral untuk daerah yang dibatasi oleh satu kurva.

a. Daerah antara Kurva dan Sumbu Koordinat

Perhatikan gambar luasan di bawah ini.

R sebagaimana terlihat pada gambar di atas adalah luasan yang dibatasi oleh kurva-kurva `y=f(x)`, `x=a`, `x=b`. Dengan menggunakan integral tertentu luas luasan dinyatakan dengan

`A(R)=\int_{a}^{b}f(x)dx`

Jika luasan terletak di bawah sumbu-x, maka integral tertentu di atas bernilai negatif, karena luas daerah tidak mungkin bilangan negatif maka nilai integral tersebut dimutlakkan. Sehingga luas luasan daerah negatif dinyatakan dalam bentuk

`A(R)=\int_{a}^{b}-f(x)dx=|\int_{a}^{b}f(x)dx|`

Untuk menghitung luas luasan dengan integral tertentu dapat diikuti langkah-langkah sebagai berikut:

1. Sketsakan daerah yang akan ditentukan luasnya sehingga tampak jelas batas-batasnya dan mudah dilihat.
2. Buatlah garis-garis yang sejajar sumbu-x atau sumbu-y, selanjutnya irislah (bagi) luasan dalam bidang yang disebut partisi dan berikan nomor pada masing-masing partisi yang terbentuk.
3. Aproksimasikan luas masing-masing partisi tertentu dengan menganggapnya sebagai sebuah persegi panjang.
4. Jumlahkan aproksimasi dari luas masing-masing partisi pada luasan yang telah dibentuk.
5. Dengan menggunakan limit dari jumlah luas partisi diatas dengan lebar masing-masing partisi menuju 0, maka diperoleh integral tertentu yang merupakan luas luasan.

Contoh 1

Susunlah integral untuk daerah di bawah kurva `y=1+\sqrt{x}` di antara `x=0` dan `x=4`.

3. Aproksimasikan luas irisan khas: `\Delta A_{i}=(1+\sqrt{x_{i}})\Delta x_{i}`

4. Jumlahkan: `A(R)\approx \sum_{i=1}^{n}(1+\sqrt{x_{i}})\Delta x_{i}`

5. Ambil limit: `A(R)= \int_{0}^{4}(1+\sqrt{x_{i}})dx`

Jika kita telah memahami prosedur lima langkah ini, kita dapat menyingkatnya menjadi tiga langkah: iris, aproksimasikan, integrasikan.

2. Aproksimasikan:

`\Delta A(R)\approx (1+\sqrt{x})\Delta x`

3. Integrasikan:

`A(R)= \int_{0}^{4}(1+\sqrt{x})dx`

Contoh 2

Segitiga ABC terletak pada `XOY`, titik-titik sudutnya dinyatakan dalam koordinat kartesius yaitu `A(0,0)`, `B(3,0)`, dan `C(3,7)`. Dengan menggunakan integral tertentu tentukan luas segitiga ABC.

Jawab:

Persamaan garis AC dinyatakan dengan rumus

`\frac{y-y_{A}}{y_{C}-y_{A}}=\frac{x-x_{A}}{x_{C}-x_{A}}`

`\Leftrightarrow \frac{y-0}{7-0}=\frac{x-0}{3-0}`

`\Leftrightarrow 3y=7x`

`\Leftrightarrow y=\frac{7}{3}x`

Sehingga luas yang dicari dinyatakan dengan 

`A(R)=\int_{a}^{b}f(x)dx`

         `=\int_{0}^{3}\frac{7}{3}xdx`

         `=[\frac{7x^{2}}{6}]_{0}^{3}`

         `=\frac{7(3)^{2}}{6}-\frac{7(0)^{2}}{6}`

         `=\frac{7(9)}{6}-0`

         `=10,5` satuan luas

Contoh 3

Gambar di atas menyajikan grafik fungsi `f(x)=sinx` di antara `x=0` dan `x=2\pi`. Hitunglah luas di antara grafik `f(x)` dan sumbu-x pada `[0,2\pi]`.

Jawab:

Luas di antara grafik fungsi `f(x)` dan sumbu-x pada `[0,2\pi]` dihitung dengan memisahkan daerah asal `sinx` menjadi dua bagian: interval `[0,\pi]` dimana fungsi bernilai positif, dan interval `[\pi,2\pi]` dimana fungsi bernilai negatif.

`\int_{0}^{\pi} sinx dx=[-cosx]_{0}^{\pi}=-(cos\pi -cos0)=-(-1-1)=2`

`\int_{\pi }^{2\pi} sinx dx=[-cosx]_{\pi }^{2\pi}=-(cos2\pi -cos\pi )=-(1-(-1))=-2`

Integral kedua bernilai negatif. Luas di antara grafik dan sumbu-x diperoleh dengan cara menjumlahkan nilai mutlak,

Luas (Area) `=2+|-2|=2+2=4`

Contoh 4

Carilah luas daerah di antara sumbu-x dan grafik `f(x)=x^{3}-x^{2}-2x,-1\leq x\leq 2`

Jawab:

Pertama, carilah pembuat nol dari `f`.

`f(x)=0`

`\Leftrightarrow x^{3}-x^{2}-2x=0`

`\Leftrightarrow x(x^{2}-x-2)=0`

`\Leftrightarrow x(x+1)(x-2)=0`

Jadi, pembuat nol dari `f` adalah `x=0, -1, 2` (lihat gambar)

Karena pembuat nol membagi `[-1,2]` menjadi dua subinterval, yaitu `[-1,0]`, ketika `f\geq 0`, dan `[0,2]`, ketika `f\leq  0`. Kita mengintegrasikan `f` pada setiap subinterval dan menjumlahkan nilai mutlak dari integral yang dihitung.

`\int_{-1}^{0}(x^{3}-x^{2}-2x)dx=[\frac{x^{4}}{4}-\frac{x^{3}}{3}-x^{2}]_{-1}^{0}`

`=0-(\frac{1}{4}+\frac{1}{3}-1)`

`=-(-\frac{5}{12})`

`=\frac{5}{12}`

`\int_{0}^{2}(x^{3}-x^{2}-2x)dx=[\frac{x^{4}}{4}-\frac{x^{3}}{3}-x^{2}]_{0}^{2}`

`=(\frac{2^{4}}{4}-\frac{2^{3}}{3}-2^{2})-0`

`=4-\frac{8}{3}-4`

`=-\frac{8}{3}`

Luas total diperoleh dengan menjumlahkan nilai mutlak dari integral yang dihitung.

Luas total `=\frac{5}{12}+|-\frac{8}{3}|=\frac{5}{12}+\frac{8}{3}=\frac{37}{12}`

Contoh 5

Tentukan luas luasan yang dibatasi oleh kurva `f(x)=4-x^{2}` dan sumbu-x pada interval `[-2,2]`.

Jawab:

Berdasarkan gambar di atas, luasan yang diketahui berada di atas sumbu-x sehingga luasnya dapat dinyatakan dengan menggunakan integral, yaitu:

`A(R)=\int_{a}^{b}f(x)dx`

         `=\int_{-2}^{2}(4-x^{2})dx`

         `=2\int_{0}^{2}(4-x^{2})dx`

         `=2[4x-\frac{x^{3}}{3}]_{0}^{2}`

         `=2[4(2)-\frac{2^{3}}{3}-0]`

         `=2[\frac{16}{3}]`

         `=\frac{32}{3}`

note: 

`f(x)=4-x^{2}` adalah fungsi genap karena `f(x)=f(-x)`

`f(x)=4-x^{2}`

`f(-x)=4-(-x)^{2}=4-x^{2}`

Contoh 6

Tentukan luas luasan yang dibatasi oleh kurva `x=y^{2}` dan garis `x=4`.

Jawab:

Dengan cara yang sama luas luasan di atas dinyatakan dengan

`A(R)=\int_{0}^{4}f(x)dx+\int_{0}^{4}-f(x)dx`

         `=\int_{0}^{4}\sqrt{x}dx+\int_{0}^{4}-(-\sqrt{x})dx`

         `=\int_{0}^{4}\sqrt{x}dx+\int_{0}^{4}\sqrt{x}dx`

         `=2\int_{0}^{4}\sqrt{x}dx`

         `=2\int_{0}^{4}x^{\frac{1}{2}}dx`

         `=2[\frac{2x^{\frac{3}{2}}}{3}]_{0}^{4}`

         `=2(\frac{2(4)^{\frac{3}{2}}}{3}-0)`

         `=2(\frac{16}{3})`

         `=\frac{32}{3}`

Selanjutnya, perhatikan gambar luasan berikut ini:

Luasan pada gambar di atas dibatasi oleh kurva `x=f(y)`, `y=c`, `y=d`, dan `x=0`. Dengan integral tertentu luasan yang berada disebelah kanan sumbu-y dinyatakan dalam bentuk

`A(R)=\int_{c}^{d}f(y)dy`

Jika gambar terletak disebelah kiri sumbu-y, maka integral tertentu di atas bernilai negatif. Karena luas daerah tidak mungkin bilangan negatif maka nilai integral tersebut dimutlakkan, sehingga diperoleh:

`A(R)=\int_{c}^{d}-f(y)dy=|\int_{c}^{d}f(y)dy|`

Contoh 7

Tentukan luas luasan yang dibatasi oleh kurva `x=y^{2}`, `y=-2`, `y=2`.

Jawab:

Luasan `x=y^{2}`, `y=-2`, `y=2` dapat digambarkan sebagai berikut:

Sehingga luas luasan tersebut adalah

`A(R)=\int_{c}^{d}f(y)dy`

         `=\int_{-2}^{2}y^{2}dy`

         `=2\int_{0}^{2}y^{2}dy`

         `=2[\frac{y^{3}}{3}]_{0}^{2}`

         `=2[\frac{(2)^{3}}{3}-0]`

         `=2(\frac{8}{3})`

         `=\frac{16}{3}`

b. Daerah antara Dua Kurva

Daerah antara dua kurva adalah luasan yang pembatasnya adalah `y=f (x)` dan `y=g(x)` dengan `f(x)=g(x)` pada selang `[a,b]`. Seperti halnya luasan yang dibatasi oleh satu kurva, luasan yang dibatasi dua kurva dapat berupa luasan positif dan luasan negatif. Dengan demikian aturan menentukan luasan dengan integral pada luasan yang dibatasi satu kurva juga berlaku untuk luasan yang dibatasi oleh dua kurva.

Perhatikan gambar berikut ini.

`\Delta A\approx (f(x)-g(x))\Delta x`

Sehingga luasan dinyatakan dengan:

`A(R)=\int_{a}^{b}(f(x)-g(x))dx`

Rumus di atas berlaku untuk luasan di atas sumbu-x, jika luasannya disebelah kanan sumbu-y, maka luas luasan yang dibatasi oleh dua kurva dinyatakan dengan

`A(R)=\int_{c}^{d}(f(y)-g(y))dy`

Contoh 8

Carilah luas daerah di antara kurva `y=x^{4}` dan `y=2x-x^{2}`

Jawab:

Mencari titik-titik perpotongan kedua persamaan:

  `x^{4}=2x-x^{2}`

`\Leftrightarrow x^{4}+x^{2}-2x=0`

`\Leftrightarrow x(x^{3}+x-2)=0`

`\Leftrightarrow x(x-1)(x^{2}+x+2)=0`

`\Leftrightarrow x=0`

       `x=1`

       `x\notin \mathbb{R}`

Jadi, titik-titik perpotongan kedua persamaan adalah ` x=0,1`

Sehingga diperoleh,

`\Delta A(R)=(2x-x^{2}-x^{4})\Delta x=(-x^{4}-x^{2}+2x)\Delta x`

`A(R)=\int_{0}^{1}(-x^{4}-x^{2}+2x)dx`

         `=[-\frac{x^{5}}{5}-\frac{x^{3}}{3}+x^{2}]_{0}^{1}`

         `=(-\frac{1^{5}}{5}-\frac{1^{3}}{3}+1^{2})-0`

         `=-\frac{1}{5}-\frac{1}{3}+1`

         `=\frac{7}{15}`

         `\approx 0,46` satuan luas