Pada topik-topik sebelumnya, kita telah membahas mengenai integral tertentu dengan berbagai macam sifatnya. Integral tertentu dapat digunakan untuk menentukan selesaian masalah-masalah praktis dalam kehidupan nyata. Beberapa diantara penggunaan integral adalah menentukan luas suatu luasan, menghitung volume benda pejal, menentukan panjang busur suatu kurva yang telah ditentukan persamaannya, dan menentukan luas permukaan benda putar. Nah, pembahasan kita kali ini secara khusus membahas tentang luas daerah bidang datar.
Luasan didefinisikan sebagai suatu daerah dalam bidang `XOY` dengan persamaan `y=f(x)` atau `x=f(y)`, atau `y=f(x), x=f(y)` yang berbatasan dengan sumbu-sumbu koordinat atau garis yang sejajar sumbu koordinat. Luasan dalam bidang dapat dikelompokkan menjadi luasan positif dan luasan negatif. Luasan positif adalah luasan dengan persamaan `y=f(x)` dan sumbu-sumbu koordinat yang terletak di atas sumbu-x atau luasan dengan persamaan `x=f(y)` dan sumbu-sumbu koordinat yang terletak disebelah kanan sumbu-y. Teman-teman dapat melihat gambar luasan positif yang dimaksud dalam gambar di bawah ini.
Luasan negatif adalah luasan dengan persamaan `y=f(x)` dan sumbu-sumbu koordinat yang terletak di bawah sumbu-x atau luasan dengan persamaan `x=f(y)` dan sumbu-sumbu koordinat yang terletak disebelah kiri sumbu-y. Berikut ini gambar luasan negatif tersebut.
Luasan positif dan negatif sebagaimana telah dijelaskan di atas, pembatasan juga dapat terjadi bukan hanya satu kurva tetapi dapat juga berupa dua kurva sekaligus, misalnya `y_{1}=f(x)` dan `y_{2}=g(x)`. Pembahasan ini diawali dengan menentukan luas luasan menggunakan integral untuk daerah yang dibatasi oleh satu kurva.
a. Daerah antara Kurva dan Sumbu Koordinat
Perhatikan gambar luasan di bawah ini.
R sebagaimana terlihat pada gambar di atas adalah luasan yang dibatasi oleh kurva-kurva `y=f(x)`, `x=a`, `x=b`. Dengan menggunakan integral tertentu luas luasan dinyatakan dengan
`A(R)=\int_{a}^{b}f(x)dx`
Jika luasan terletak di bawah sumbu-x, maka integral tertentu di atas bernilai negatif, karena luas daerah tidak mungkin bilangan negatif maka nilai integral tersebut dimutlakkan. Sehingga luas luasan daerah negatif dinyatakan dalam bentuk
`A(R)=\int_{a}^{b}-f(x)dx=|\int_{a}^{b}f(x)dx|`
Untuk menghitung luas luasan dengan integral tertentu dapat diikuti langkah-langkah sebagai berikut:
- Sketsakan daerah yang akan ditentukan luasnya sehingga tampak jelas batas-batasnya dan mudah dilihat.
- Buatlah garis-garis yang sejajar sumbu-x atau sumbu-y, selanjutnya irislah (bagi) luasan dalam bidang yang disebut partisi dan berikan nomor pada masing-masing partisi yang terbentuk.
- Aproksimasikan luas masing-masing partisi tertentu dengan menganggapnya sebagai sebuah persegi panjang.
- Jumlahkan aproksimasi dari luas masing-masing partisi pada luasan yang telah dibentuk.
- Dengan menggunakan limit dari jumlah luas partisi diatas dengan lebar masing-masing partisi menuju 0, maka diperoleh integral tertentu yang merupakan luas luasan.
Contoh 1
Susunlah integral untuk daerah di bawah kurva `y=1+\sqrt{x}` di antara `x=0` dan `x=4`.
4. Jumlahkan: `A(R)\approx \sum_{i=1}^{n}(1+\sqrt{x_{i}})\Delta x_{i}`
5. Ambil limit: `A(R)= \int_{0}^{4}(1+\sqrt{x_{i}})dx`
Jika kita telah memahami prosedur lima langkah ini, kita dapat menyingkatnya menjadi tiga langkah: iris, aproksimasikan, integrasikan.
2. Aproksimasikan:
`\Delta A(R)\approx (1+\sqrt{x})\Delta x`
3. Integrasikan:
`A(R)= \int_{0}^{4}(1+\sqrt{x})dx`
Contoh 2
Segitiga ABC terletak pada `XOY`, titik-titik sudutnya dinyatakan dalam koordinat kartesius yaitu `A(0,0)`, `B(3,0)`, dan `C(3,7)`. Dengan menggunakan integral tertentu tentukan luas segitiga ABC.Jawab:
Persamaan garis AC dinyatakan dengan rumus
`\frac{y-y_{A}}{y_{C}-y_{A}}=\frac{x-x_{A}}{x_{C}-x_{A}}`
`\Leftrightarrow \frac{y-0}{7-0}=\frac{x-0}{3-0}`
`\Leftrightarrow 3y=7x`
`\Leftrightarrow y=\frac{7}{3}x`
Sehingga luas yang dicari dinyatakan dengan
`A(R)=\int_{a}^{b}f(x)dx`
`=\int_{0}^{3}\frac{7}{3}xdx`
`=[\frac{7x^{2}}{6}]_{0}^{3}`
`=\frac{7(3)^{2}}{6}-\frac{7(0)^{2}}{6}`
`=\frac{7(9)}{6}-0`
`=10,5` satuan luas
Contoh 3
Gambar di atas menyajikan grafik fungsi `f(x)=sinx` di antara `x=0` dan `x=2\pi`. Hitunglah luas di antara grafik `f(x)` dan sumbu-x pada `[0,2\pi]`.
Jawab:
Luas di antara grafik fungsi `f(x)` dan sumbu-x pada `[0,2\pi]` dihitung dengan memisahkan daerah asal `sinx` menjadi dua bagian: interval `[0,\pi]` dimana fungsi bernilai positif, dan interval `[\pi,2\pi]` dimana fungsi bernilai negatif.
`\int_{0}^{\pi} sinx dx=[-cosx]_{0}^{\pi}=-(cos\pi -cos0)=-(-1-1)=2`
`\int_{\pi }^{2\pi} sinx dx=[-cosx]_{\pi }^{2\pi}=-(cos2\pi -cos\pi )=-(1-(-1))=-2`
Integral kedua bernilai negatif. Luas di antara grafik dan sumbu-x diperoleh dengan cara menjumlahkan nilai mutlak,
Luas (Area) `=2+|-2|=2+2=4`
Contoh 4
Carilah luas daerah di antara sumbu-x dan grafik `f(x)=x^{3}-x^{2}-2x,-1\leq x\leq 2`
Jawab:
Pertama, carilah pembuat nol dari `f`.
`f(x)=0`
`\Leftrightarrow x^{3}-x^{2}-2x=0`
`\Leftrightarrow x(x^{2}-x-2)=0`
`\Leftrightarrow x(x+1)(x-2)=0`
Jadi, pembuat nol dari `f` adalah `x=0, -1, 2` (lihat gambar)
Karena pembuat nol membagi `[-1,2]` menjadi dua subinterval, yaitu `[-1,0]`, ketika `f\geq 0`, dan `[0,2]`, ketika `f\leq 0`. Kita mengintegrasikan `f` pada setiap subinterval dan menjumlahkan nilai mutlak dari integral yang dihitung.
`\int_{-1}^{0}(x^{3}-x^{2}-2x)dx=[\frac{x^{4}}{4}-\frac{x^{3}}{3}-x^{2}]_{-1}^{0}`
`=0-(\frac{1}{4}+\frac{1}{3}-1)`
`=-(-\frac{5}{12})`
`=\frac{5}{12}`
`\int_{0}^{2}(x^{3}-x^{2}-2x)dx=[\frac{x^{4}}{4}-\frac{x^{3}}{3}-x^{2}]_{0}^{2}`
`=(\frac{2^{4}}{4}-\frac{2^{3}}{3}-2^{2})-0`
`=4-\frac{8}{3}-4`
`=-\frac{8}{3}`
Luas total diperoleh dengan menjumlahkan nilai mutlak dari integral yang dihitung.
Luas total `=\frac{5}{12}+|-\frac{8}{3}|=\frac{5}{12}+\frac{8}{3}=\frac{37}{12}`
Contoh 5
Tentukan luas luasan yang dibatasi oleh kurva `f(x)=4-x^{2}` dan sumbu-x pada interval `[-2,2]`.
Jawab:
Berdasarkan gambar di atas, luasan yang diketahui berada di atas sumbu-x sehingga luasnya dapat dinyatakan dengan menggunakan integral, yaitu:
`A(R)=\int_{a}^{b}f(x)dx`
`=\int_{-2}^{2}(4-x^{2})dx`
`=2\int_{0}^{2}(4-x^{2})dx`
`=2[4x-\frac{x^{3}}{3}]_{0}^{2}`
`=2[4(2)-\frac{2^{3}}{3}-0]`
`=2[\frac{16}{3}]`
`=\frac{32}{3}`
note:
`f(x)=4-x^{2}` adalah fungsi genap karena `f(x)=f(-x)`
`f(x)=4-x^{2}`
`f(-x)=4-(-x)^{2}=4-x^{2}`
Contoh 6
Jawab:
Dengan cara yang sama luas luasan di atas dinyatakan dengan
`A(R)=\int_{0}^{4}f(x)dx+\int_{0}^{4}-f(x)dx`
`=\int_{0}^{4}\sqrt{x}dx+\int_{0}^{4}-(-\sqrt{x})dx`
`=\int_{0}^{4}\sqrt{x}dx+\int_{0}^{4}\sqrt{x}dx`
`=2\int_{0}^{4}\sqrt{x}dx`
`=2\int_{0}^{4}x^{\frac{1}{2}}dx`
`=2[\frac{2x^{\frac{3}{2}}}{3}]_{0}^{4}`
`=2(\frac{2(4)^{\frac{3}{2}}}{3}-0)`
`=2(\frac{16}{3})`
`=\frac{32}{3}`
Selanjutnya, perhatikan gambar luasan berikut ini:
Luasan pada gambar di atas dibatasi oleh kurva `x=f(y)`, `y=c`, `y=d`, dan `x=0`. Dengan integral tertentu luasan yang berada disebelah kanan sumbu-y dinyatakan dalam bentuk
`A(R)=\int_{c}^{d}f(y)dy`
Jika gambar terletak disebelah kiri sumbu-y, maka integral tertentu di atas bernilai negatif. Karena luas daerah tidak mungkin bilangan negatif maka nilai integral tersebut dimutlakkan, sehingga diperoleh:
`A(R)=\int_{c}^{d}-f(y)dy=|\int_{c}^{d}f(y)dy|`
Contoh 7
Jawab:
Luasan `x=y^{2}`, `y=-2`, `y=2` dapat digambarkan sebagai berikut:
Sehingga luas luasan tersebut adalah
`A(R)=\int_{c}^{d}f(y)dy`
`=\int_{-2}^{2}y^{2}dy`
`=2\int_{0}^{2}y^{2}dy`
`=2[\frac{y^{3}}{3}]_{0}^{2}`
`=2[\frac{(2)^{3}}{3}-0]`
`=2(\frac{8}{3})`
`=\frac{16}{3}`
b. Daerah antara Dua Kurva
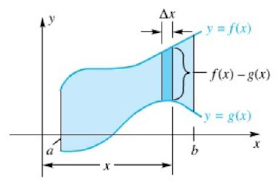
Daerah antara dua kurva adalah luasan yang pembatasnya adalah `y=f (x)` dan `y=g(x)` dengan `f(x)=g(x)` pada selang `[a,b]`. Seperti halnya luasan yang dibatasi oleh satu kurva, luasan yang dibatasi dua kurva dapat berupa luasan positif dan luasan negatif. Dengan demikian aturan menentukan luasan dengan integral pada luasan yang dibatasi satu kurva juga berlaku untuk luasan yang dibatasi oleh dua kurva.
Perhatikan gambar berikut ini.
`\Delta A\approx (f(x)-g(x))\Delta x`
Sehingga luasan dinyatakan dengan:
`A(R)=\int_{a}^{b}(f(x)-g(x))dx`
Rumus di atas berlaku untuk luasan di atas sumbu-x, jika luasannya disebelah kanan sumbu-y, maka luas luasan yang dibatasi oleh dua kurva dinyatakan dengan
`A(R)=\int_{c}^{d}(f(y)-g(y))dy`
Contoh 8
Carilah luas daerah di antara kurva `y=x^{4}` dan `y=2x-x^{2}`
Jawab:
Mencari titik-titik perpotongan kedua persamaan:
`x^{4}=2x-x^{2}`
`\Leftrightarrow x^{4}+x^{2}-2x=0`
`\Leftrightarrow x(x^{3}+x-2)=0`
`\Leftrightarrow x(x-1)(x^{2}+x+2)=0`
`\Leftrightarrow x=0`
`x=1`
`x\notin \mathbb{R}`
Jadi, titik-titik perpotongan kedua persamaan adalah ` x=0,1`
Sehingga diperoleh,
`\Delta A(R)=(2x-x^{2}-x^{4})\Delta x=(-x^{4}-x^{2}+2x)\Delta x`
`A(R)=\int_{0}^{1}(-x^{4}-x^{2}+2x)dx`
`=[-\frac{x^{5}}{5}-\frac{x^{3}}{3}+x^{2}]_{0}^{1}`
`=(-\frac{1^{5}}{5}-\frac{1^{3}}{3}+1^{2})-0`
`=-\frac{1}{5}-\frac{1}{3}+1`
`=\frac{7}{15}`
`\approx 0,46` satuan luas


















0 komentar:
Posting Komentar